材料力学の公式集です。
材料力学計算 - 公式集
公式集
断面二次モーメント
| 形状 | 面積 : A | 図心からの距離 : e | 断面二次モーメント : I | 断面係数 : Z |
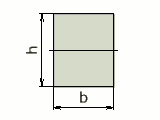 |
bh | h / 2 | bh³ / 12 | bh² / 6 |
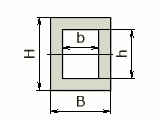 |
BH - bh | H / 2 | (BH³ - bh³)/ 12 | (BH³ - bh³)/ 6H |
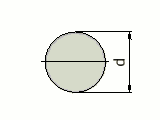 |
πd² / 4 | d / 2 | πd⁴/ 64 | πd³ / 32 |
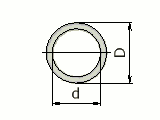 |
π(D² - d²)/ 4 | D / 2 | π(D⁴ - d⁴ )/ 64 | π(D⁴ - d⁴ )/ 32D |
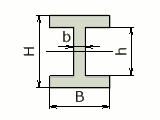 |
BH -(B - b)h | H / 2 | (BH³ -(B - b)h³)/ 12 | (BH³ -(B - b)h³)/ 6H |
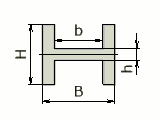 |
BH - b(H - h) | H / 2 |
((B - b)H³ + bh³)/ 12 |
((B - b)H³+ bh³)/ 6H |
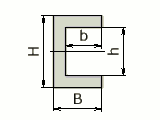 |
BH - bh | H / 2 | (BH³ - bh³)/ 12 | (BH³ - bh³)/ 6H |
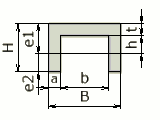 |
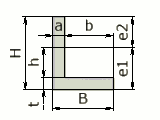
BH - b(e2 + h) | e1 = (aH² + bt²)/ (2(aH + bt)) e2 = H - e1 |
(Be1³ - bh³ + ae2³)/ 3 | I / e1 : I / e2 |
 |
BH - b(e2 + h) | e1 = (aH² + bt²)/ (2(aH + bt)) e2 = H - e1 |
(Be1³ - bh³ + ae2³)/ 3 | I / e1 : I / e2 |
はりのたわみ
|
はりと荷重状態 |
たわみ角 : θ | 曲げモーメント : M | たわみ : δ |
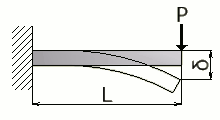 片持ちはり - 集中荷重 |
PL² / 2EI | PL | PL³ / 3EI |
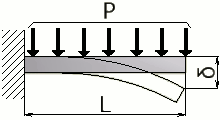 片持ちはり - 等分布荷重 |
PL³ / 6EI | PL² / 2 | PL⁴ / 8EI |
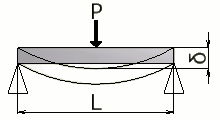 単純支持はり - 集中荷重 |
PL² / 16EI | PL / 4 | PL³ / 48EI |
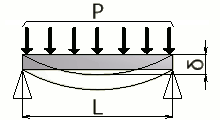 単純支持はり - 等分布荷重 |
PL³ / 24EI | PL²/ 8 | 5PL⁴ / 384EI |
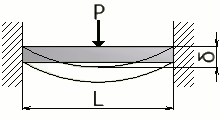 両端固定はり - 集中荷重 |
PL² / 64EI | PL / 8 | PL³ / 192EI |
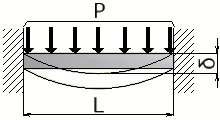 両端固定はり - 等分布荷重 |
√3PL³ / 384EI | PL²/ 12 | PL⁴ / 384EI |
柱の座屈
|
座屈荷重 : Pk = Cπ²EI / L² |
L = 柱の長さ E = ヤング率 I = 断面二次モーメント λ = 細長比 = L / k(断面二次半径)(断面二次半径 : k = √I / A(断面積)) C = 端末条件係数 : 両端固定 = 4 / 両端回転 = 1 / 回転 - 固定 = 2.046 / 自由 - 固定 = 0.25 |
||||
|
座屈応力 : σc = Cπ²E / λ² |
|||||
|
座屈応力 : σc = σD / 1 + αλ² |
σD,α,λ = 材質による定数 |
||||
|
定数/材料 |
錬鉄 | 軟鋼 | 硬鋼 | 木材 | |
|
σD(MPa) |
245 | 333 | 481 | 49 | |
|
α |
1/9 000 | 1/7 500 | 1/5 000 | 1/700 | |
|
λ(相当細長比) |
< 110 | < 90 | < 85 | < 60 | |
|
テトマイヤーの式 |
|||||
|
座屈応力 : σc = σD( 1 - αλ) |
σD,α,λ = 材質による定数 |
||||
|
定数/材料 |
錬鉄 | 軟鋼 | 硬鋼 | 木材 | |
|
σD(MPa) |
297 | 304 | 329 | 28.7 | |
|
α |
0.00426 | 0.00368 | 0.00185 | 0.00626 | |
|
λ(相当細長比) |
< 112 | < 105 | < 90 | < 100 | |
|
ジョンソンの式 |
|||||
|
座屈応力 : σc = σy( 1 - (σy / 4π²E)λ²) |
σy = 降伏応力 E = ヤング率 λ(相当細長比) |
||||
